الرياضيات في دقيقة، أرقامٌ معقّدة

تاريخ التسجيل : 07/09/2018

هل أحضرت الفُشار؟ هلاخترتَ مقعدًا جيدًا؟ هل تجلسُ بشكلٍ مريح؟ إذًا دع المرحَ يبدأ!

الرياضيات تقدّم بفخر

لقد تعجبنا جميعًا بالصور المنتَجة من قبل الكومبيوتر الشبيهة بالحياة الواقعية بشكل لا يصدق في الأفلام.

لكن ما لا يدركه معظمنا هو أنّ الديناصورات من فيلم جوراسيك بارك وعجائب فيلم سيد الخواتم –وخصوصا دور الشخصية غولوم في الفيلم– لم تكن من الممكن صنعها من دون الرياضيات.

ولكن كيف يتم تصنيع كل هذه الصور المدهشة؟

رسومات الحاسوب والرؤية الحاسوبية هي مواضيع ضخمة.

في هذه المقالة سوف نلقي نظرة مبسطة على بعض الرياضيات التي نحتاجها للوصول إلى المنتج النهائي.

أولًا سنقوم بخلق العالم الذي يُنظَر اليهفي الفيلم، وبعد ذلك سنحضره للحياة.

إعداد المشهد

الخطوة الأولى في صنع فيلم تم إنشاؤه بواسطة الكمبيوتر هي إنشاء الشخصيات في القصة والعالم الذي يعيشون فيه.

كلٌّ من هذه الكائنات يتم تمثيلها على شكل مستوي يتكون من مجموعة من المضلعات المتصلة (عادة مثلثات).

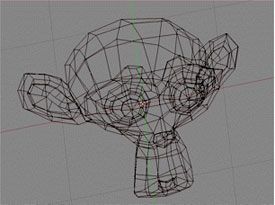
الرياضيات في دقيقة، أرقامٌ معقّدة Trianglesurface_web

الرياضيات في دقيقة، أرقامٌ معقّدة Trianglesurface_web

يتم تصميم الكائنات الأولى على شكل هياكل عظمية على شكل أسلاك تتكون من مضلعات بسيطة مثل المثلثات.

يتم تخزين رؤوس كل مثلث في ذاكرة الكمبيوتر.

من المهم أن تعرف أي جانب من المثلث يقع على الجزء الخارجي من الكائن أو الشخصية.

يتم ترميز هذه المعلومات حسب الترتيب الذيتمّ تخزين الرؤوس فيه، وذلك وفقًا لقاعدة مسماراليد اليمنى (قم بتدوير أصابع يدك اليمنى حول المثلث حسب ترتيب رؤوس المثلث).

هناك طريقة واحدة فقط للقيام بذلك ونتيجة لذلك سوف ينتهي الأمر بإبهامكعلى جانب واحد من المثلث، وهذا الجانب هو الجزء الخارجي للمثلث.

إذا حاولت فعل هذا مع نموذجِ ما، سوف تجد أن الاتجاه الخارجي (يسمى العيار الخارجي) للمثلث (A,B,C)هو فيالحقيقة الاتجاه المعاكس لذلك(A,C,B).

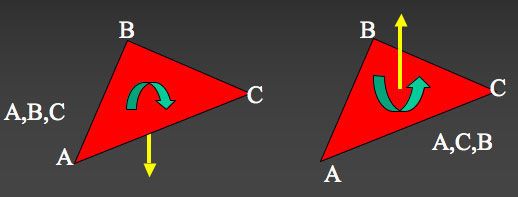
الرياضيات في دقيقة، أرقامٌ معقّدة Rhrule_web

الرياضيات في دقيقة، أرقامٌ معقّدة Rhrule_web

المعيار الخارجي لـ (A,B,C) هو في الاتجاه المعاكس لـ (A,C,B) كما موضح في قاعدة مسمار اليد اليمنى

الآن سطح الكائن الذي صنعناه هو عبارة عن شبكة سلكية من المثلثات، نحن الآن على استعداد لتلوين كل من مكوناته.

من المهم هناأن نلتقط الإضاءة من المشهدالذي نمثّله بواقعية، ويتم ذلك باستخدام عملية تسمى التتبع الإشعاعي (Ray Tracing).

بدءًا من وجهة نظرنا الحالية، نتتبع الأشعة إلى الوراء نحو الكائن ونسمح له بعكس الإشعاع قبالة ذلك.

إذا كان الشعاع من عيننا يعكُس قبالة الوجه (واحد من مثلثات الشبكة السلكية) ويتقاطع مع مصدر الضوء، نقوم بتضليل هذا الوجه بلون مشرق بحيث يبدو مضاءً من مصدر ضوءٍ. إذا كان شعاع المنعكَس لا يتطابق مع مصدر الضوء، نقوم بتلميس الوجه بلون أغمق.

الرياضيات في دقيقة، أرقامٌ معقّدة Rayfacet

الرياضيات في دقيقة، أرقامٌ معقّدة Rayfacet

قم بتتبع شعاع من وجهة نظرك إلى وجوه المثلث. هل يعكس ذلك ويتقاطع مع مصدر الضوء؟

لتتبّع الأشعة مرة أخرى إلى وجه معين، نحن بحاجة إلى وصف السطح رياضيًّا، وحل المعادلات الهندسية التي تنطوي على الشعاع والمستوى الذي تمّ وصفه قبل هذا.

ويتم ذلك باستخدام مصفوفات ثلاثية الأبعاد.

نحن نفرض نظام تنسيق ثلاثي الأبعاد على مشهدنا مع الأصل –و النقطة (0،0،0)- وضعت في وجهة نظرنا.

يشير المتجه v=(a,b,c) الآن إلى السهم الذي يبدأ من الأصل وينتهي عند النقطة بالتنسيق مع a, b و cيمكننا الأن ضرب V فيأي عدد، على سبيل المثال 2، وفقا للقاعدة

لذلك v2 هو سهم يشير في نفس الاتجاه كماv ولكن بضعف الطول.

الآن ننظر إلى التعبير لامد اv، حيث لامدا هو متغير، وبعبارة أخرى لامدا هي أي رقم حقيقي.

هذا لم يعد يشيرإلى سهم لطول معين، حيث أصبح الطول متغيرًا، ولكن فقط باتجاه السهم.

بعبارة أخرى، يصف هذا التعبير الرياضي السطر الذي يحتوي على المتجهv، ويصفُ خطًّا مستقيما كالآتي (الشعاع –الانبعاث من نقطة الأصل–النقطة التي ننظر منها- الاتجاه الذي يعطيه المتجه v).

المستوي الذي تم تحديده من قبل الوجوه المثلثية يمكن أن يمثل ثلاثة معلومات:

موقع واحد من ثلاثة رؤوس للمثلث، نسميها الرأسa_1، جنبًا إلى جنب مع مصفوفة ثلاثية تمثل الخط من a_1 إلى قمة الرأس a_2 والخط من a_1 إلى الرأسa_3.

المربع أدناه يعطي معادلات الشعاع بدءًا من نقطة نظرنا والمستوى الذي قدّمه الوجه لمعرفة ما إذا كان وأين يتقاطع الشعاع مع الوجه وحساب معادلة الأشعة المنعكسة، نحن بحاجة الأن إلى حل المعادلات التي تنطوي على هذين التعبيرين.

معادلة الشعاع، حيث لامدا هي رقم حقيقي و vهي مصفوفة ثلاثية:معادلة المستوي التي تم تحددها في وجوه المثلث مع الرأسa_1، a_2 و a_3:

تقنية التتبع الإشعاعي، يمكن أن تنتج مشاهد واقعية لكنّها بطيئة جدًا.

هذا مقبول الى حدٍّ ما لإنتاج الأفلام المصممةبالكمبيوتر، ولكنّ المشكلة تحدث عندما تحتاج الإضاءة للتغيير في الوقت الحقيقي، كما هو الحال في ألعاب الكمبيوتر.

الظواهر المعقدة مثل الظلال، المؤثرات والانعكاساتالمتعدّدة من الصعب أن تتمثل ديناميكيًا بأساليب رياضية أكثر احترافية، على سبيل المثال تقنيةالحساب المسبق للنقل الإشعاعي وتقنية الراديو سيتي تستخدم هنا ايضًا.

الرياضيات في دقيقة، أرقامٌ معقّدة Neverwinter_web

الرياضيات في دقيقة، أرقامٌ معقّدة Neverwinter_web

تتطلب ألعاب الحاسوب مثل دوم 3 و نيفروينتر نايتز إضاءة ديناميكية

الرياضيات في دقيقة، أرقامٌ معقّدة Doom3_web

يتطلّب الأمر القليل من الخيال فقط

ريثما يتم تعيين المشهد لدينا، ونحن ننتظر المخرج لإطلاق شارة العمل وشخصياتنا لبدء التحرك.

الآن سوف ندرس الرياضيات التي يمكن أن تجلب صورنا إلى الحياة.

واحدة من أكثر الحركات الأساسية التي يمكن أن يؤدّيها الكائن هيالدوران حول محور معين وعلى زاوية معينة.

الهندسة التنسيقية تعطينا الأدوات اللازمة لحساب موقف كل نقطة على الكائن بعد أن أتمّ استدارته، ولكن من المهم أن تكون هذه الأدوات فعّالة وسريعة في آنٍ واحد.

للعثور على هذهِ الأدوات، دعونا نعودُ خطوة إلى الوراء، إلى حصة الرياضيات في المدرسة.

نحن نعلم أن العدد 25 يمتلك جذرين تربيعين اثنين هما +5 و -5 كما .

ولكن ما هو الجذر التربيعي ل -25؟ للعثور على الجذر التربيعي للأرقام السالبة، اضطر علماء الرياضيات إلى إنشاء رقم جديد يسمى i، حيث i ^ 2 = -1. كما نجد ان .

إدخال i يعني أن المعادلات مثل يمكن الآن حلها.

وأرقام من نموذجات مثل ،التي تدعى الأرقام المعقدة، أصبحت أداة مهمة في الرياضيات. ولكن الكثير من الناس لم يكونوا سعداء بهذا الرقم الخيالي الجديد الغريب i.

وأخيرا في 1806 قدم عالم الرياضيات جان روبرت أرغاند تفسيرًا هندسيًّا للأعداد المعقدة و i.أرغاند ربَط الأرقام المعقدة مع نقاط في المستوي مع العدد الحقيقي 1 موضوعًا على محور واحد، ورقم وهمي اخر موضوعٌ من جهة أخرى.

على سبيل المثال الرقم 1 + i يتوافق مع النقطة (1،1). وبصفة عامة، فإن العدد المعقد a + ib يتوافق مع النقطة (a,b).

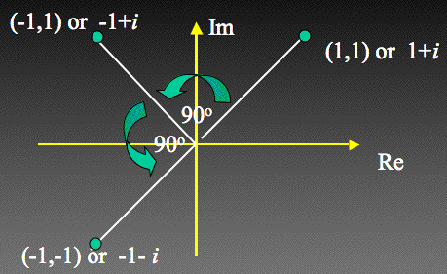
الرياضيات في دقيقة، أرقامٌ معقّدة Mathem

الرياضيات في دقيقة، أرقامٌ معقّدة Mathem

الضرب بالأعداد المركبة لديها وصف هندسي – التدوير.

أدرك أرغاند أن ناتج الضرب بالأعداد المعقدة له وصف هندسي ألا هو التدوير.

دعونا ننظر إلى ما يحدث إذا ضربنا 1 + i، ممثلة في النقطة (1،1) من قبل i:

والتي تمثلها النقطة (-1،1)، بدوران 90 درجة مضروبة بـ i مرة أخرى يعطي:

والتي هي النقطة (-1، -1)، بدوران 90 درجة مرة أخرى.

مضروبة بـi والتي تمثل تعليمات للتدوير بنسبة 90 درجة! في الواقع، أي دوران، وليس فقط 90 درجة واحدة، يمكن أن يتحقق باستخدام الضرب بـ عدد معقد.

لننتقل الأن إلى الأشكال ثلاثية الأبعاد

عالم الرياضيات السير ويليام روان هاميلتونالإبن الأكثر شهرة في كلية ترينيتي فيدوبلين.

كرّس العقدين الماضيين من حياته للبحث عن وسيلة لتمثيل مصفوفات ثلاثية الأبعاد بطريقة مماثلة للطريقة التي تمكّن الأعداد المعقدة من محاكاة الدوران في مصفوفات ذي بُعدَين.

في نهاية حياته اكتشف هاملتون الجواب، في شكل شيء دعاه هو بالكواترونيونس او "ارقام الأشكال”.

حيث وa0 ,a1 ,a2 هي أرقام حقيقية.

وللقيام بذلك، فإن iو j و k تمثل الأسطح الأساسية في فضاءٍ ثلاثي الأبعادِ:

وهذا يمثل i للمستويyz، ويمثل j للمستويxy ويمثل k للمستويxz، مع القيم الخارجية للاتجاهات x، -y و z على التوالي.

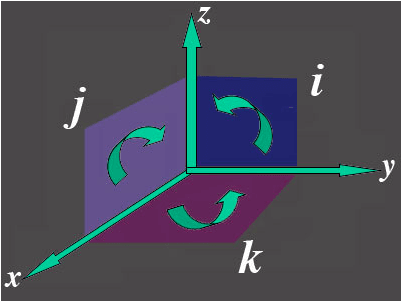
الرياضيات في دقيقة، أرقامٌ معقّدة 123-3

i و j و k يمكن تفسيرها هندسيا باعتبارها عنصرا مستويًا يمثل ثلاثة ابعادِ

لنفترض أننا نود أن نقوم بتدوير النقطة ، من خلال زاوية حول المحور من الأصل الذي يٌعطى من قبل.

نحن نبني هنا كوارتونيونسين اثنينq_1 و q_2 باستخدام هذا المحور المتجه الىbبزاوية .

وثم يمكننا مضاعفة a(معبرًا عنهاكمزيج من متجهات للوحدة في الاتجاهاتxو y و z )بواسطة هاتين الفترتين (باتباع قواعد خاصة لضرب المستوياتi و j و k ووحدات رؤوس المثلث) لإعطاء:

اتضح أنّ النقطة a’ "تعطى كناتج للضرب، هي بالضبط النقطة التي تحصل عليها عند التدوير حول محور معين من خلال زاوية!

لذلك يمكن استخدام الأعداد المعقدة لوصف الدوران في المستوي المسطح، يمكن استخدام الكواترونيونس لوصف التدوير في فضاء ثلاثي الأبعادِ.

نظرة هامرتون المتألقة عن ضرب الأعداد المعقدة، ريثما كان يسير تحت هذا الجسر في دبلن، بينت أنها أنجح طريقة لتدوير الكائنات في ثلاثة أبعاد.

ولكن لم يكن الجميع سعيدا بهذه الطريقة الجديدة في الضرب. الفيزيائي اللورد كلفن، قال عنالكواترونيونس: "… على الرغم من جمال الطريقة العبقري، كان الشر مصيرًا لأولئك الذين لمست ايديهم هذه الكائنات بأي شكل من الأشكال!”

مما يبعث على القلق على البعض أنه عندما تتضاعف اثنتان من هذه الرباعيات، يعتمد الجواب في النهاية على الترتيب الذي تتضاعف فيه، وهي خاصية تسمى عدم التبادلية.

على سبيل المثال، قاعدة ضرب هاملتون، يمكن أن تُظهِر في و . ومع ذلك يمكن أن تٌظهِر أيضًا أنّه عندما يتم التعامل معi، yو kكمستويات أساسية، فإنّ الخصائص التي كانت مقلقة جدا لكلفن ومعاصريه، تتّبع مباشرة من الرياضيات.

جلب الصور إلى الحياة

يستخدم اختراع هاملتون الآن في العديد من تطبيقات الرسوم لنقل الأجسام أو إنشاء الحركة.

اثنين من أهم الأدوات في رسومات الكمبيوتر هي التشوّهات والاستيفاء.

الاستيفاء وتقنية الإطار الرئيسي تتضمن تحديد الشكل الأولي، والتشطيب للكائن، وموقعه، وجعل الكمبيوتر يحدد المراحل بينهما، كما هو مبين في الصورة أدناه.

شكل إبريق الشاي يتغير تدريجيا على سلسلة من الإطارات.

التشويه او تقنية اعادة التشكيل الرسومية هي وسيلة لخلق كائنات معقّدة من كائنات أبسط منها.

يمكن اشتقاق لقطة لقطعة قماش تسقط من على سطح مكور معاد تشكيله، من خلال التلاعب الرياضي بنفس المشهد الذي ينطوي على نطاق عادي للمشهد.

كل من التشوه والاستيفاء تتطلب تقنيات رياضية سريعة ومستقرة وطرق كواترنيونتوفر هذا كله.

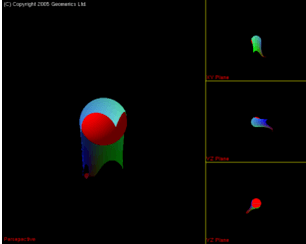
الرياضيات في دقيقة، أرقامٌ معقّدة 22222

قطعة القماش التي تسقط على الشكل الكروي المبين أعلاه يمكن أن تُصممَ باستعمال قوانين الفيزياء

الرياضيات في دقيقة، أرقامٌ معقّدة 44444

ومن ثم يتم التلاعب بها لإعطاء قطعة القماش سقطة من فوق الشكل الدائرة

جعل الشخصية غولوم أكثر واقعية

التقنيات المذكورة أعلاه هي أدوات أساسية للرسوم المتحركة الكلاسيكية، ونحن سعداء بها جدًا لشخصيات الرسوم المتحركة.

ولكن عندما تستخدمها لتحريك البشر، يمكننا تحديد الفرق على الفور.

لإنشاء حركة واقعية، يتطلب الأمر التقاطًا للحركة.

العديد من الشخصيات، مثل غولوم من النسخة السينمائية لفيلم سيد الخواتم، يتم بناؤها باستخدام تقنيات التقاط الحركة.

ويتم ذلك عن طريق ربط عاكسات لأشخاص حقيقيين في نقاط محورية من الجسم، على الرأس، الكتفين، المرفقين، الركبتين، وما إلى ذلك.

يتم تصوير الأفراد من قبل كاميرات متعددة ويتم تخزين المشهد المتغير من العاكسات على جهاز كومبيوتر، ثم يتم تركيب هيكل عظمي على البيانات ثلاثية الأبعاد، وأخيرا يتم استخدام جميع التقنيات المذكورة أعلاه لوضع اللحم على العظام وخلق الحياة، التنفس، وتحريك الشخصية.

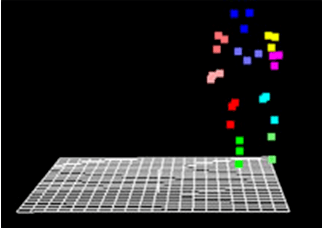
الرياضيات في دقيقة، أرقامٌ معقّدة 55555

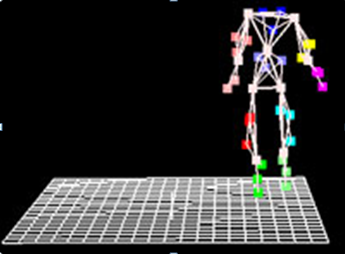
الرياضيات في دقيقة، أرقامٌ معقّدة Capture-42

إذا كنت قد بقيت في أي وقت مضى لمشاهدة كامل الاعدادات لفيلم معين عليك أن تكون على يقين بأن مجموعة كبيرة من المواهب الإبداعية ساهمت بجعل الفيلم ناجحًا منهم: الكتاب والمخرجين والممثلين ومصممي الأزياء، وبناء المسرح والقائمة تطول.

ولكن لدينا اسمٌ واحد غالبًا ما يغيب عن تلك القائمة، إنّه الرياضيات.

العديد من أفلام اليوم لميكن من الممكن صنعها من دون هندسة تعقب الأشعة أو تقنية الكواترونيونس للكائنات في الفضاء.

لذلك في المرة القادمة التي تجلس فيها في مقعدك في السينما للاستمتاع بفيلم ما، ارفع الفشار للرياضيات، النجم الخفي للفيلم.